Approach 1. Flux creep Pinning energy   U = Uc ln( j / jc ),   jc= const where E = vB,    v = vc exp[ -U(j) / kT ],	j / jc
Approach 2. Nonlinear current-voltage curve Electric field   E = Ec ( j / jc ) n,   jc= const   B(x)-movie     E(x)-movie     Abstract & Text Flux creep simulations online - main page	j / jc	coordinate across the strip

The transport current through the initially zero-field-cooled strip increases linearly in time, dI/dt= 0.001 I_cv_c / (2w), where 2w is the strip width;   U_c / kT = n = 5;

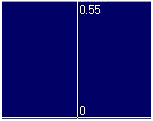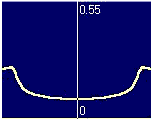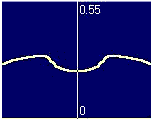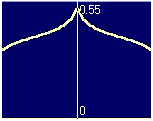
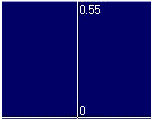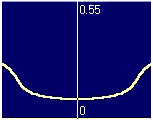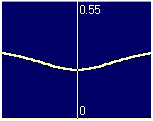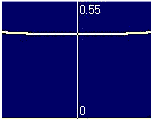
Common in distributions:   The distributions are qualitatively similar to each other, and also to that expected for the Bean model [PRB 48, 12893 (1993), PRB 49, 9802 (1994)] where the current density is largest in the flux penetrated regions near the strip edges. As the current increases, the flux penetrates deeper. Finally, the central flux-free region shrinks, and the current becomes distributed more uniformly.

Differences:   First, in the penetrated regions near the edge the slope of j(x) is opposite in two different approaches. Second, only in approach 1 there is a central peak (where B=0) in j(x) at high currents. These differences can be briefly explained as follows. In the E-j approach, j(x) follows E(x) and, thus, decreases monotonously from the edges towards the center. In the flux diffusion approach, however, one has v(j)=E/B, which means that j tends to be larger where |B| is smaller. In particular, j(x) is relatively small at the edges where |B| is maximal, but divergent in the annihilation zone where B=0.