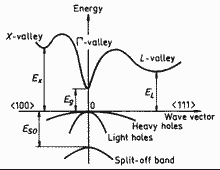
Important minima of the conduction band and maxima of the valence band..
For details see Goldberg Yu.A. & N.M. Schmidt (1999) .
Porod and Ferry (1983)

| Ga0.47In0.53As | GaxIn1-xAs | Remarks | Referens | |
| Energy gaps, Eg |
0.74 eV | (0.36+0.63x+0.43x2) eV | 300 K | Goetz et al.(1983) |
| Energy gaps, Eg |
(0.4105+0.6337x+0.475x2) eV | 2 K | Goetz et al.(1983) | |
| Electron affinity | 4.5 eV | (4.9-0.83x) eV | 300 K | |
| Conduction band | ||||
| Energy separation between X valley and top of the valence band EX |
1.33 eV | (1.37-0.63x+1.16x2) eV | 300 K | Goetz et al.(1983) |
| Energy separation between L valley and top of the valence band EL |
1.2 eV | (1.08-0.02x+0.65x2) eV | 300 K | Goetz et al.(1983) |
| Effective conduction band density of states | 2.1·1017 cm-3 | see Temerature dependences | ||
| Valence band | ||||
| Energy separation of spin-orbital splitting Eso | *** | *** | ||
| Effective valence band density of states | 7.7·1018 cm-3 | see Temerature dependences | ||
| Intrinsic carrier concentration | 6.3·1011 cm-3 | see Temerature dependences | ||
 |
GaxIn1-xAs (zinc blende, cubic). Band structure
Important minima of the conduction band and maxima of the valence band.. For details see Goldberg Yu.A. & N.M. Schmidt (1999) . |
 |
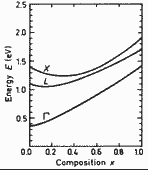
GaxIn1-xAs. Energy gap Eg Energy
separations between Γ- ,X-, and L -conduction band minima and top
of the valence band vs. composition parameter x. Porod and Ferry (1983) |
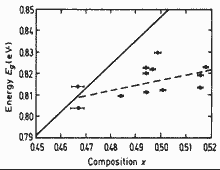 |
GaxIn1-xAs. Energy band gap Eg of unstrained
(solid line) and strained (dashed line and experimental points) vs. composition
parameter x. Solid line is calculated according to Eg= (0.4105+0.6337x+0.475x2) eV. Experimental points are obtained at 4K. Kuo et al.(1985) |
 |
Brillouin zone of the face centered cubic lattice, the Bravais lattice of the diamond and zincblende structures. |
 |
Brillouin zone of the hexagonal lattice. |
| Eg (x,T)= 0.42 + 0.625x -[5.8/(T+300)-4.19
/(T+271)]·10-4T2x- - 4.19·10-4T2/(T+271) +0.475x2 (eV) |
(eV) | GaxIn1-xAs | Paul et al.(1991) | |
| Eg (x,T)= Eg (0) + (6x2-
8.6x +5.2)·10-4 T2/(337x2-
455x +196) |
GaxIn1-xAs on Ga As | Karachevtseva et al.(1994) | ||
| Eg (x,T)= 0.42 + 0.625x -[5.8/(T+300)-4.19
/(T+271)]·10-4T2x- - 4.19·10-4T2/(T+271) +0.475x2 (eV) |
(eV) | GaxIn1-xAs | ||
| where T is temperature in degrees K |
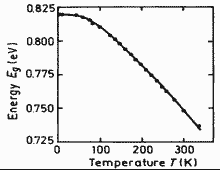 |
Ga0.47In0.53As. Energy gap Eg of vs. temperature Points are experimental data. Solid line is theoretical calculation. Eg(0)=821.5 ± 0.2 meV. Zielinski et al.(1986) |
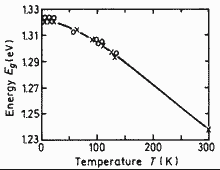 |
Ga0.87In0.13As. Energy gap Eg of vs. temperature Points are experimental data. Solid line -- 1.321 - 4.1·10-4 T2/(T+139) Karachevtseva et al.(1994) |
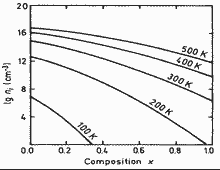 |
GaxIn1-xAs. Intrinsic carrier concentration
vs. temperature for GaxIn1-xAs. T = 100K; 200K; 300K; 400K; 500K; Paul et al.(1991) |
| Eg (0.47,P)~= (0.796+10.9x 10-3 ·P -30x10-6 ·P2) eV | 80K, Ga0.47In0.53As | x=0.47 | Lambkin and Dunstan (1988) |
| Eg (0.47,P)~= (0.733+11.0x 10-3 ·P -27x10-6 ·P2) eV | 300K, Ga0.47In0.53As | x=0.47 | |
| Eg (0.0, P)~= (Eg (0)+4.8x 10-3 ·P) eV | 300K, InAs | x=0. | |
| Eg (1.0, P)~= (Eg (0)+12.6x 10-3 ·P -37.7x10-6 ·P2) eV | 300K, GaAs | x=1. |
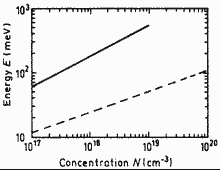 |
Ga0.47In0.53As. Energy gap narrowing Eg vs.
donor (solid line) and acceptor (dashed
line) doping density solid line -- donor doping density; dashed line -- acceptor doping density Jain et al. (1990) |
| ΔEg ~= (A ·N1/3 10-9 +B ·N1/4 10-7 +C ·N1/2 10-12) meV | 300K, Ga0.47In0.53As | x=0.47 | |
| where | |||
| n : A=15.5; B=1.95; C=159 | 300K, Ga0.47In0.53As | x=0.47 | |
| p : A= 9.2; B=3.57; C=3.65 | 300K, Ga0.47In0.53As | x=0.47 | |
| N -- carrier concentration in cm-3 |
| Referens | ||||||
| Conduction band discontinuity | ΔEv =(ΔEg -ΔEv) eV | Shur (1990) | ||||
| Valence band discontinuity | ΔEc = (0.44 ΔEgg) eV | Shur (1990) | ||||
| where ΔEgg
(eV) = [1.247y + 1.5(1-x) - 0.4(1-x)2] (eV)
is the difference between Γ-valleys in GaxIn1-xAs and AlyGA1-yAs . |
||||||
| Energy gap Eg discontinuity : | ΔEg = ΔEgg | for y<0.45 | ||||
| Energy gap Eg discontinuity : | ΔEg = 0.476 +0.125y + 0.143y2 +1.5(1-x) - 0.4(1-x)2 | for y>0.45 | ||||
| Band discontinuities | ΔEv ~= 0.38 eV ΔEc ~= 0.22 eV |
at Ga0.47In0.53As/InP heterointerface |
Adachi (1992); Hybertsen (1991) |
|||
| Band discontinuities | ΔEv ~= 0.2 eV ΔEc ~= 0.52 eV |
at Ga0.47In0.53As/Al0.48In0.52As heterointerface |
Adachi (1992); Hybertsen (1991) |
|||
| ΔEc /ΔEg = [0.653 + 0.1(1-x)] eV | at GaxIn1-xAs/AlxIn1-xAs
heterointerface |
Wolak et al.(1991) | ||||
| Effective Electron Masses | Remarks | Referens | |
| Effective electron mass me= mΓ | 0.023 -0.037x +0.003x2 mo | GaxIn1-xAs; 300K; for Γ - valley |
Goldberg Yu.A. & N.M. Schmidt (1999) |
| Effective electron mass me | mΓ= 0.041 mo at n= 2x·1017
cm-3 mΓ= 0.074 mo at n= 6x·1018 cm-3 |
Ga0.47In0.53As; x=0.47 |
Pearsall (1982) |
| mL = 0.29 mo ; ( L - valley ) mX = 0.68 mo ; ( X - valley ) |
Ga0.47In0.53As; x=0.47 |
Pearsall (1982) |
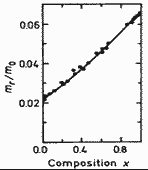 |
GaxIn1-xAs. Electron effective mass vs. concentration
x for GaxIn1-xAs; 300K Adachi (1992) |
| Effective Masses for Zinc Blende GaN | Remarks | Referens | |
| Effective hole masses (heavy) mh | mh ~= (0.41 -0.1x) mo | GaxIn1-xAs; 300K; | Goldberg Yu.A. & N.M. Schmidt (1999) |
| Effective hole masses (light) mlp | mlp ~= (0.026 -0.056x ) mo
|
GaxIn1-xAs; 300K; | |
| Effective hole masses (split-off band) ms | mso ~= 0.15 mo | GaxIn1-xAs; 300K; |
| Ionization energies of Shallow Donors |
Remarks | |||
| Sn, Ge, Si, C |
~ 5 meV |
Ga0.47In0.53As; x=0.47 |
Goldberg Yu.A. & N.M. Schmidt (1999) | |
| Sn, Ge, Si, S, Se, Te |
> 1 meV |
InAs; x=0 | ||
| Sn, Ge, Si, S, Se, Te |
~ 6 meV |
GaAs; x=1 | ||
| Ionization energies of Shallow Acceptor |
||||
| Mg |
~ 25 meV |
Ga0.47In0.53As; x=0.47 |
Goldberg Yu.A. & N.M. Schmidt (1999) | |
| Zn |
~ 20 meV |
Ga0.47In0.53As; x=0.47 | ||
| Cd |
~ 30 meV |
Ga0.47In0.53As; x=0.47 | ||
| Mn |
~ 50 meV |
Ga0.47In0.53As; x=0.47 | ||
| Fe |
~ 150 meV |
Ga0.47In0.53As; x=0.47 | ||
| (above valence band), 280, 370, and 440 below conduction band |
||||
| Mg |
~ 25 meV |
GaxIn1-xAs; 0<x<1 | ||
| Be |
~ 25 meV |
GaxIn1-xAs; 0<x<1 | ||
| Cd |
~ 8-20 meV |
GaxIn1-xAs; 0<x<1 | ||
| (above valence band), 280, 370, and 440 below conduction band |
||||
| Sn-10; Ge-14; Si-20; Cd-15; Zn-10 meV |
InAs; x=0 | |||
| C - 20, Si - three acceptor levels ~ 30, 100,
and 220, Ge - 30, Zn - 25, Sn - 20. |
GaAs; x=1 | |||