Физика магнитных наноструктур

Что называется магнитными наноразмерными структурами? Какие новые эффекты существуют в этих структурах? Какими теоретическими моделями они описываются и какие области применения магнитных наноструктур? Об этом рассказано на этой странице сайта.

Согласно существующей в настоящее время терминологии наноразмерными называются те структуры, которые содержат одномерные, двумерные или трехмерные составляющие элементы с размерами меньшими 100 нм. Если наноразмерные включения имеют магнитный момент, то такие структуры называются магнитными.

Структуры, содержащие наноразмерные ферромагнитные пленки и магнитные металлические частицы, обладают рядом свойств и особенностей, существенно отличающих их от объемных аморфных и кристаллических материалов. Особенности наноразмерных магнитных структур проявляются в их магнитных свойствах, распространении спиновых волн, электронном транспорте, диэлектрической и магнитной проницаемостях, магнитосопротивлении, в спиновом транспорте и в эффектах спиновой инжекции. Особые свойства магнитных наноструктур позволяют их рассматривать в качестве перспективных материалов для изготовления приборов на спиновых волнах, нового класса радиопоглощающих покрытий, эффективных спиновых инжекторов в спинтронных приборах, ячеек памяти и высокочувствительных магнитных сенсоров.

Диаграммная техника

Исследование квантовых систем, состоящих из ферромагнитных наночастиц, и электронных систем, в которых значительное влияние на свойства оказывает взаимодействие спинов, в полной мере не решены, в первую очередь, из-за отсутствия математических моделей и методов, которые бы адекватно описывали процессы со спиновыми взаимодействиями, происходящие на наноразмерном масштабе.
В наносистемах эти процессы могут характеризоваться сильными локальными взаимодействиями во внутренней области нанообъектов и корреляционными эффектами между разными фазами и подструктурами. Одним из эффективных теоретических методов, применяемых для исследования сильно взаимодействующих систем, является диаграммная техника, основанная на разложении функций Грина.
Для изучения наносистем и сильнокоррелированных систем возникает необходимость обобщения диаграммной техники Фейнмана на квантовые системы с произвольной внутренней Ли-групповой динамикой. Используя диаграммную технику, можно найти спектры квазичастичных возбуждений, вычислить вероятности переходов, определить температурные зависимости термодинамических потенциалов, найти параметры релаксации возбуждений. Построение диаграммной техники, которая описывает модели с произвольной внутренней Ли-групповой динамикой и учитывает топологию квантовых систем, проведено в [ 1, 2]. Подробнее

Уравнения Ландау-Лифшица

При переходе в наномасштабную область феноменологические уравнения Ландау-Лифшица перестают правильно описывать спиновые системы и требуют уточнения. Это происходит по нескольким причинам.
Во-первых, пространственная дисперсия, которая в феноменологических уравнениях описывается производными по пространственным переменным, должна быть заменена членами с суммированием по конечному числу спинов на наноразмерном масштабе.
Во-вторых, для наноразмерных спиновых систем энергетический промежуток между спинволновыми модами составляет значительную величину. Это приводит к существенному изменению способа описания диссипации спиновых волн.
Для получения обобщенных уравнений Ландау-Лифшица должна быть рассмотрена модель Гейзенберга с обменным и магнитным дипольным взаимодействиями. Собственная релаксация спинволновых возбуждений в модели Гейзенберга определяется магнитным дипольным взаимодействием.
В ферромагнитных пленках наноразмерной толщины (в пленках Y₃Fe₅O₁₂ толщина должна быть меньше 60 nm в области частот 1 ― 20 GHz) процесс слияния спинволновых мод, дающий основной вклад в релаксацию, запрещен и будут наблюдаться слабозатухающие спиновые волны. Наличие таких волн открывает возможность построения спинволновых приборов наноразмерного масштаба (фильтров, линий задержек), работающих в СВЧ диапазоне и обладающих малыми потерями [3, 2]. Подробнее

В ансамбле ферромагнитных наночастиц, помещенных в аморфную диэлектрическую матрицу, наблюдаются аномально большие величины коэффициента затухания спин-волновых возбуждений, значительно превосходящих значения собственной релаксации спинволновых возбуждений в модели Гейзенберга. Эта релаксация получила название спин-поляризационной релаксации [4].
При этом типе релаксации спин ферромагнитных наночастиц взаимодействует со спинами неспаренных электронов, локализованных на дефектах аморфной матрицы. Основным свойством спин-поляризационной релаксации является уменьшение коэффициента затухания спиновых возбуждений с ростом концентрации магнитных гранул. Подробнее

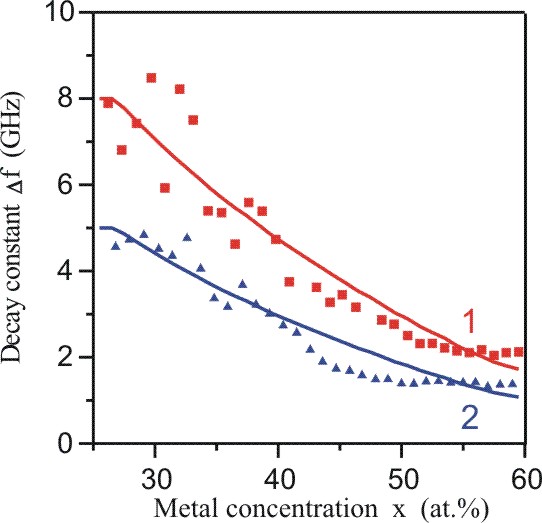Рис. 1. Коэффициент затухания спинволновых возбуждений Δf гранулированной структуры (a-SiO2)100-x(Co0.4Fe0.4B0.2)x в зависимости от концентрации металлической фазы x на частоте 4.8 GHz. 1 ― без отжига 2 ― после отжига при 400 C. Сплошные линии ― теоретические зависимости, рассчитанные при среднем количестве соседей n = 5 и расстоянии 1.3 nm от границ гранул до локализованных состояний в матрице SiO2

Коллективные спинволновые возбуждения в гранулированных структурах с магнитными наночастицами

В гранулированных структурах с магнитными наночастицами наблюдаются не только спинволновые возбуждения одиночных наночастиц, но и коллективные спинволновые возбуждения [5].
При этом распределение спиновой ориентации наночастиц может быть произвольным - от полностью разупорядоченного до ферромагнитного. Спиновая разупорядоченность в гранулированных структурах с ферромагнитными наночастицами приводит к существенному изменению дисперсионных кривых спиновых волн и к появлению дополнительных ветвей (Рис. 2). Подробнее

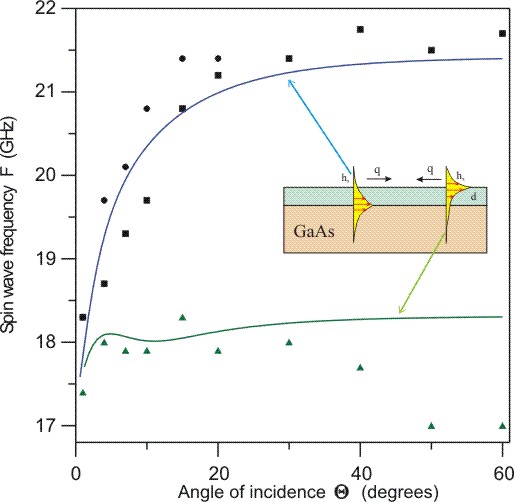Рис. 2. Дисперсионные кривые поверхностных спиновых волн, распространяющихся в пленке (SiO2)100-xCox толщиной 600 nm с концентрацией наночастиц Co x = 83 at.%. Внешнее магнитное поле H = 3 kOe, намагниченность насыщения 4πM = 9.82 kOe. hx - профиль x-компоненты переменного магнитного поля спиновой волны. Экспериментальные данные получены А. Сташкевичем из Бриллюэновского рассеяния. Θ ― угол падения света c λ = 514 nm, волновой вектор спиновой волны q = 4πsinΘ /λ .

Спинволновая спектроскопия

Главными факторами, влияющими на дисперсию спиновых волн в гранулированных наноструктурах, являются проводимость и магнитные параметры структуры. Эти факторы по-разному изменяют форму дисперсионных кривых, что дало возможность определения их магнитных и электрических характеристик из дисперсионных зависимостей спиновых волн и позволило развить метод спинволновой спектроскопии [5, 6, 7] (Рис. 3). Подробнее

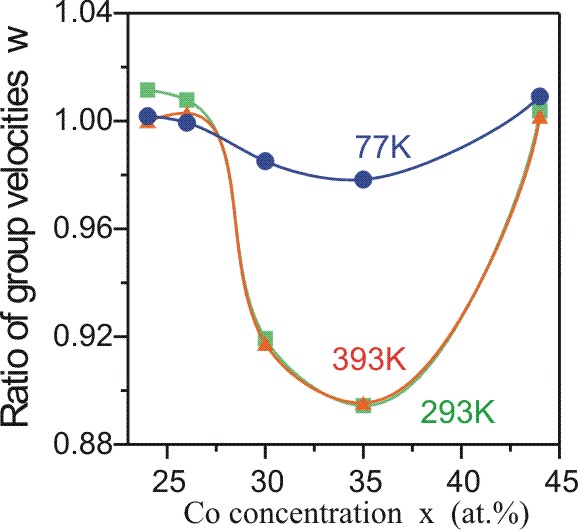Рис. 3. Изменение w групповой скорости спиновой волны в YIG пленке, взаимодействующей с образцами (a-C:H)100-xCox, в зависимости от концентрации Co x при температурах 77, 293 и 393 K.

Кластерные электронные состояния

Электронный транспорт в гранулированных структурах с наноразмерными металлическими частицами (гранулами) в изолирующей матрице обладает рядом свойств, существенно отличающих эти структуры от объемных аморфных и кристаллических материалов. Свойства гранулированных структур обусловлены:

1. Малыми размерами взаимно изолированных наночастиц. Малый размер металлических наночастиц приводит к эффектам макроскопического квантования заряда и явлению кулоновской блокады.
   
2. Туннелированием электронов между наночастицами. Процесс туннелирования электронов между частицами, который существенно зависит от наличия дефектов и примесей в диэлектрической матрице, приобретает характер резонансного туннелирования, зависящего от температуры, и определяет не только проводимость системы и разброс ее величины в широких пределах при изменении концентрации металлической фазы, но и температурную зависимость проводимости.
3. Большая разница в проводимости приводит к существованию области перколяционного порога и проявляется в смене характера проводимости при изменении концентрации металлической фазы.

Попытка объяснить экспериментальные зависимости проводимости, не укладывающиеся в классическую перколяционную теорию, а также обнаруженные значительные изменения диэлектрической проницаемости и увеличение потерь с ростом температуры привела к необходимости модификации классической перколяционной теории и введения кластерных электронных состояний (КЭС, Рис. 4) Подробнее

[8, 9]

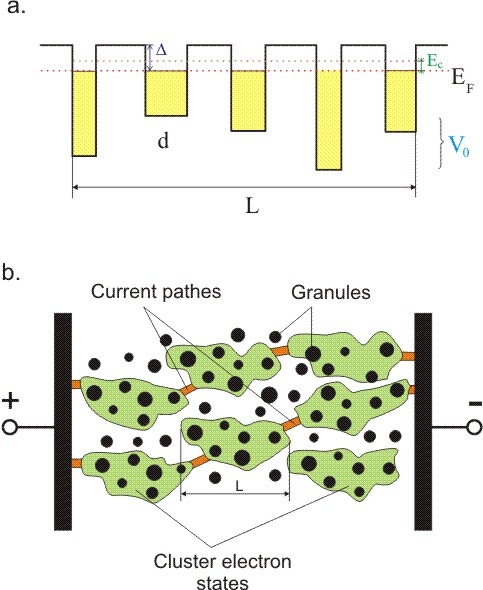Рис. 4. (a) Энергетическая структура квантовых ям, на которых локализовано кластерное электронное состояние (КЭС). Случайное распределение глубин V0 квантовых ям гранул определяется разбросом их электрических емкостей. L ― размер локализации КЭС. (b) КЭС в гранулированной структуре.

Диэлектрические свойства

Образование КЭС приводит к изменениям диэлектрической проницаемости ε в гранулированных структурах, что было экспериментально подтверждено исследованиями на пленках a-SiO₂ с наночастицами сплава (Co₄₀Fe₄₀B₂₀) и пленках a-C:H с наночастицами Cu [10, 9].
Ниже порога перколяции измерения ε дают информацию об изменениях размеров проводящих кластеров, которые изменяются под действием электрического поля и температуры (Рис. 5). В области перколяционного порога, где КЭС образует бесконечный проводящий кластер, наблюдается резкое повышение диэлектрической проницаемости. Подробнее

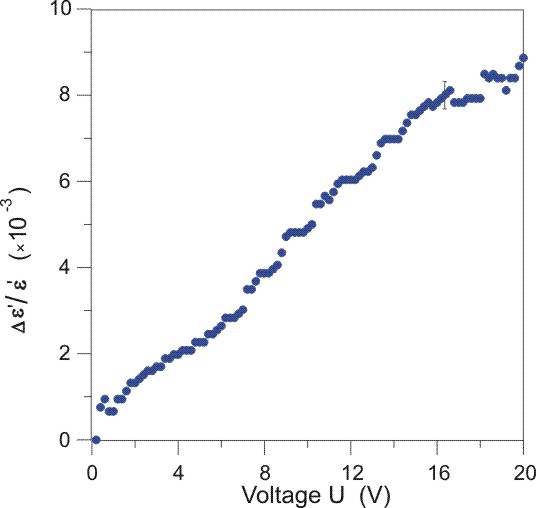Рис. 5. Изменение действительной части диэлектрической проницаемости Δεʼ/εʼ0 = (εʼ -εʼ0)/εʼ0 с ростом подаваемого на контакты напряжения U для пленки (a-C:H)84Cu16.

Радиопоглощающие покрытия

Большие величины диэлектрических и магнитных потерь в гранулированных структурах с ферромагнитными наночастицами позволили разработать многослойные тонкие широкополосные поглощающие покрытия электромагнитных волн СВЧ диапазона, которые обладают преимуществами перед покрытиями, основанными на ферритах ― по толщине, весу и частотной широкополосности поглощения (Рис. 6) [11]. Подробнее

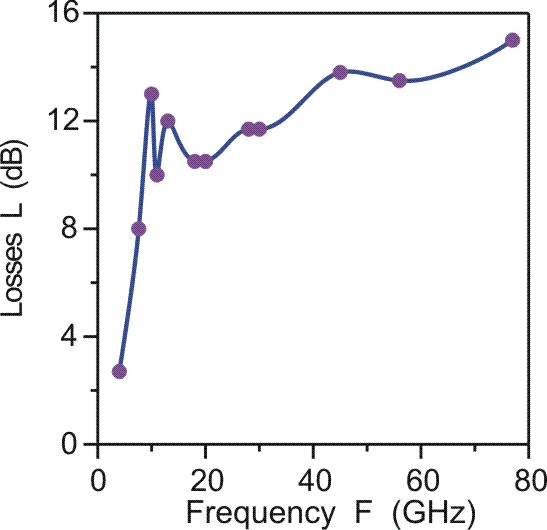Рис. 6. Частотная зависимость 5-слойного покрытия на основе гидрогенизированного углерода с наночастицами Co и Ni.

Магнитотранспортные явления

Электронный транспорт в гранулированных структурах с ферромагнитными металлическими наночастицами происходит посредством неупругого резонансного туннелирования через цепочку слаборасщепленных локализованных состояний в матрице между кластерными электронными состояниями (Рис. 7) [12]. Наблюдается как отрицательное, так и положительное магнитосопротивление. Подробнее

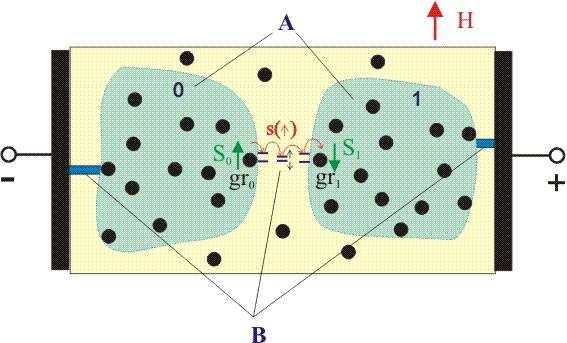Рис. 7. Электронный транспорт в магнитном поле H между двумя кластерными электронными состояниями (КЭС) 0 и 1. (A) ― КЭС; (B) ― спин-поляризованные каналы; gr0 и gr1― гранулы, с которых начинается и заканчивается цепочка локализованных состояний туннельного канала; S0, S1 ― спины гранул gr0 и gr1.

Гигантское инжекционное магнитосопротивление

Эффект гигантского инжекционного магнитосопротивления обнаружен на гетероструктурах SiO₂(Co)/GaAs, где SiO₂(Co) является гранулированной пленкой SiO₂ с наночастицами Co.
Эффект магнитосопротивления наблюдается при развитии лавинного процесса в полупроводнике и для гетероструктур SiO₂(Co)/GaAs с 71 at. % Co достигает 1000 (10⁵ %) при комнатной температуре. [13, 14, 15]
Эффект IMR имеет положительные значения и обладает температурно-пиковым характером. Температурная локализация эффекта зависит от концентрации Co и сдвигается приложенным электрическим полем (Рис. 8). Подробнее

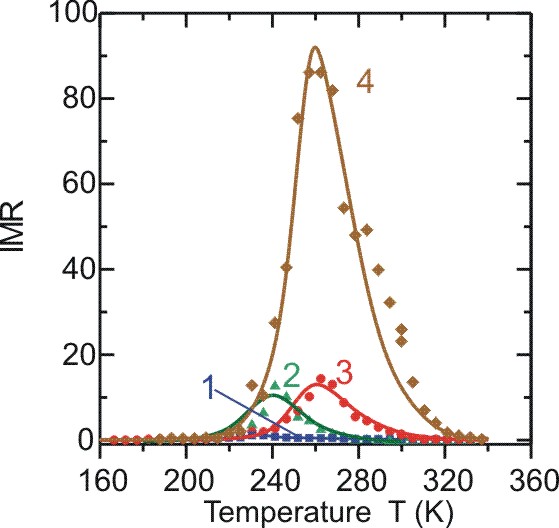Рис. 8. Температурные зависимости IMR для структуры SiO2(Co)/GaAs с x = 71 at.% Co в касательном магнитном поле H = 10 kOe при приложенных напряжениях: (1) U = 40 V (2) 50 V (3) 60 V (4) 70 V Сплошные линии ― теоретические кривые.

1. L.V. Lutsev, Diagram technique for models with internal Lie-group dynamics, J. Phys. A: Mathematical and Theoretical, 2007, Vol. 40, No. 39, pp. 11791-11814.
   
   
2. L.V. Lutsev, Diagram technique for quantum models with internal Lie-group dynamics, in: Mathematical Physics Research Developments, Editor: Morris B. Levy, (Nova Science Publishers, Inc., 2009), pp. 141-188.
   
   
3. L.V. Lutsev, Landau-Lifshitz equations and relaxation of spin wave modes in the Heisenberg model with dipole-exchange interaction, J. Phys.: Condensed Matter, 2005, Vol. 17, No. 38, pp. 6057-6080.
   
   
4. Л.В. Луцев, Спиновые возбуждения в гранулированных структурах с ферромагнитными наночастицами, ФТТ, 2002, 44(1), 97-105.
   
   
5. Л.В. Луцев, Спинволновая спектроскопия магнитных наноструктур, Наноструктуры. Математическая физика и моделирование, 2009, том 1, ╧ 1, с. 59-82.
   
   
6. Л.В. Луцев, С.В. Яковлев, В.И. Сиклицкий, Электронный транспорт в наноразмерной кластерной структуре углерод-медь, ФТТ, 2000, 42(6), 1105-1112.
   
   
7. Leonid Lutsev, Sergey Yakovlev, and Christian Brosseau, Spin wave spectroscopy and microwave losses in granular two-phase magnetic nanocomposites, Journal of Applied Physics, 2007, Vol. 101, No. 3, 034320.
   
   
8. В.И. Сиклицкий, Л.В. Луцев, М.В. Байдакова, Структура гранулированных пленок аморфного углерода с наночастицами кобальта, Письма в ЖТФ, 2002, 28 (7), 46-51.
   
   
9. Л.В. Луцев, М.Н. Копытин, А.В. Ситников, О.В. Стогней, Свойства наногранулированных композитов металл-диэлектрик в сильных электрических полях и кластерные электронные состояния, ФТТ, 2005, 47(11), 2080-2090.
   
   
10. L. V. Lutsev, N. E. Kazantseva, I. A. Tchmutin, N. G. Ryvkina, Yu. E. Kalinin, and A. V. Sitnikoff, Dielectric and magnetic losses of microwave electromagnetic radiation in granular structures with ferromagnetic nanoparticles, J. Phys.: Condensed Matter, 2003, Vol. 15, No. 22, pp. 3665-3681.
    
    
11. L.V. Lutsev, S.V. Yakovlev, T. K. Zvonareva, A.G.Alexeyev, A.P.Starostin, S.V. Kozyrev, Microwave Properties of Granular Amorphous Carbon Films with Cobalt Nanoparticles, Journal of Applied Physics, 2005, Vol. 97, No. 10, 104327.
    
    
12. Л.В. Луцев, Ю.Е. Калинин, А.В. Ситников, О.В. Стогней, Электронный транспорт в магнитном поле в гранулированных пленках аморфной двуокиси кремния с ферромагнитными наночастицами, ФТТ, 2002, 44(10), 1802-1810.
    
    
13. Л.В. Луцев, А.И. Стогний, Н.Н. Новицкий, Гигантское инжекционное магнитосопротивление в гетероструктурах арсенид галлия / гранулированная пленка с наноразмерными включениями кобальта, Письма в ЖЭТФ, 2005, 81(10), 636-641.
    
    
14. L.V. Lutsev, A.I. Stognij, and N.N. Novitskii, Giant magnetoresistance in semiconductor / granular film heterostructures with cobalt nanoparticles, Physical Review B, 2009, Vol. 80, Issue 18, 184423.
    
    
15. L.V. Lutsev, Potential barrier for spin polarized electrons induced by the exchange interaction at the interface in the ferromagnet / semiconductor heterostructure, J. Phys.: Condensed Matter, 2006, Vol. 18, No. 26, pp. 5881-5894.

Контакты

Луцев Леонид Владимирович
Лаборатория оптики полупроводников
ФТИ им. А.Ф. Иоффе
l_lutsev@mail.ru