| SiGe | | | Remarks | Referens |
Energy gaps, Egindirect
(Δ conduction
band min) | Si1-xGex |
1.12-0.41x + 0.008x2 eV | 300 K, x
< 0.85 | |
| | Si (x=0) |
1.12 eV | 300 K, x = 0. | see Si.
Band structure |
| |
Energy gaps, Egindirect
(L conduction band min) | Si1-xGex |
1.86 - 1.2x eV | 300 K, x > 0.85 | |
| | Ge (x=1) | 0.66 eV | 300 K, x
= 1. | see Ge. Band structure
|
|
| Conduction band
| | | | |
| Energy separation
EΓ1 | Si1-xGex |
4175 - (2814 ± 55)x meV | 70 K; 0 < x < 0.3, Linear Fitting
Si1-xGex
films on Si substrates | Ebner et al. (1998) |
| | Si (x=0) | 3.4 eV | 300 K | see
Si. Band structure |
| | Ge
(x=1) | 0.8 eV | 300 K | see Ge.
Band structure |
| Eg(Γ-X) | Si1-xGex |
0.8941 + 0.0421x+ 0.1691x2 | calculated | Krishnamurti
et al. (1983) |
| Eg(Γ-L) | Si1-xGex |
0.7596 + 1.0860x+ 0.3306x2 | calculated | Krishnamurti
et al. (1983) |
| Energy separation EΓ2 |
Si1-xGex | (3400 ±
7) - (300 ± 40)x meV | 70 K; 0 < x < 0.3, Linear Fitting
Si1-xGex
films on Si substrates | Ebner et al. (1998) |
| | Si (x=0) | 4.2 eV | 300 K | see
Si. Band structure |
| | Ge
(x=1) | 3.2 eV | 300 K | see Ge.
Band structure |
|
| Valence
band | | | | |
| Energy of
spin-orbital splitting Eso | Si1-xGex |
0.044 + 0.246x eV | 300 K | |
| |
Si (x=0) | 0.044 eV | 300 K, x = 0. | see
Si. Band structure |
| | Ge
(x=1) | 0.29 eV | 300 K, x = 1. | see
Ge. Band structure |
| | | | | |
| Effective conduction band density of states | Si1-xGex |
~ 2.8 x 1019cm-3 | 300 K, x < 0.85 | |
| | Si1-xGex |
~ 1.0 x 1019cm-3 | 300 K, x > 0.85 | |
| | Si (x=0) | 2.8 x 1019cm-3 | 300
K, x = 0. | see Si. Band
structure |
| | Ge (x=1) | 1.0 x
1019cm-3 | 300 K, x = 1. | see Ge.
Band structure |
| | | | | |
| Effective valence band density of states | Si (x=0) |
1.8 x 1019cm-3 | 300 K, x = 0. | see
Si. Band structure |
| | Ge
(x=1) | 0.5 x 1019cm-3 | 300 K, x
= 1. | see Ge. Band structure
|
|
| Intrinsic carrier concentration |
Si1-xGex | |
see Si1-xGex. Intrinsic
carrier concentration |
| | Si (x=0) |
1 x 1010 cm-3 | 300 K, x = 0. | see
Si. Band structure |
| | Ge
(x=1) | 2 x 1013 cm-3 | 300 K, x
= 1. | see Ge. Band structure
|
| |
| Energy Gaps vs. Composition | | | | |
| E1 | Si1-xGex |
3452 - (1345 ± 25)x meV | 70 K; 0 < x < 0.3,
Linear
Fitting
Si1-xGex films on Si substrates | Ebner
et al. (1998) |
| E'1 | Si1-xGex |
5402 ± 25 + (280 ± 120)x meV |
| E2 (X) | Si1-xGex |
4351 ± 38 + (210 ± 180)x meV |
| E2 (Σ) | Si1-xGex |
4518 ± 129 + (880 ± 600)x meV |
| Eg(Γ-X) | Si1-xGex |
0.8941 + 0.0421x+ 0.1691x2 | calculated | Krishnamurti
et al. (1983) |
| Eg(Γ-L) | Si1-xGex |
0.7596 + 1.0860x+ 0.3306x2 | calculated | Krishnamurti
et al. (1983) |
Both the valence and conduction band degeneracy
are lifted by the uniaxial [001] strain component, which leads to the following splittings
(Van de Walle and Martin, (1986)):
For higher Ge contents, the conduction band becomes Ge-like with electrons being
located at the L minimum. With the uniaxial strain component being directed along
[001], no splitting of the L minimum occurs for reasons of symmetry.
 | Si1-xGex.
Schematic diagram of the relevant band edges of Si subjected to hydrostatic
and uniaxial strain as described in equations.
Energy values apply to a tensely
strained Si quantum well on an Si1-xGex substrate with x
= 30%
Schaffler(1997) |
 | Si1-xGex.
Contour plots of the conduction ΔEc and valence ΔEv
band offsets of pseudomorphic Si1-xGex layers on cubic Si1-xsGexs
substrates over the complete range of x and xs.
The signs correspond
to an electronic energy scale, where the active layer (x) is referred to the
cubic substrate of composition xs. Exciton-corrected experimental results indicate
that for x > xs and x < 0.8, the conduction band offset is 0<ΔEc<+40
meV [Penn et al. (1999)];
that is, for
most of the (x,xs) combinations the band alignment is staggered (Type II) with
the valence band offset being always in favor of the material with the higher Ge content.
The theoretically predicted Type I region for x and xs being larger
than about 80% has not been confirmed experimentally Schaffler(1997) |
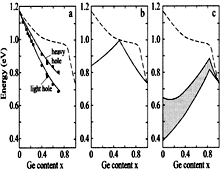
 | Si1-xGex.
Solid lines - Variation of the relevant band edges of a strained Si
layer on a cubic Si1-xsGexs substrate .
The dashed
lines correspond to the substrate bands.
LH, light holes;
HH, heavy holes;
SO, spin-orbit split holes
Schaffler(1997) |
 | Si1-xGex.
Solid lines - Variation of the relevant band edges of a strained Ge
layer on a cubic Si1-xsGexs substrate .
The dashed
lines correspond to the substrate bands. .
LH, light holes;
HH, heavy holes;
SO, spin-orbit split holes
Schaffler(1997) |








 4.82 x 1015 · M ·
(mc/m0)3/2·T3/2
(cm-3)
4.82 x 1015 · M ·
(mc/m0)3/2·T3/2
(cm-3)  + 2
+ 2 )
)  0.85).
0.85).









